ta-project-bitcoin/bitcoin-technical.md

Notefile for the technical background of the Bitcoin/Blockchain TA Project (WS 18/19)

Note: The information presented here is specifically for the Bitcoin Blockchain technology, as well as some general terms from computer science. The source for any bitcoin related stuff is the original whitepaper: Satoshi Nakamoto - Bitcoin: A Peer-to-Peer Electronic Cash System - Please also note that Satosho Nakamoto is most likely a pseudonym, nevertheless, the paper is the exact specification for the technology, and therefore relevant!

A few terms important to understand the technology

(Cryptographic) Hash <1>

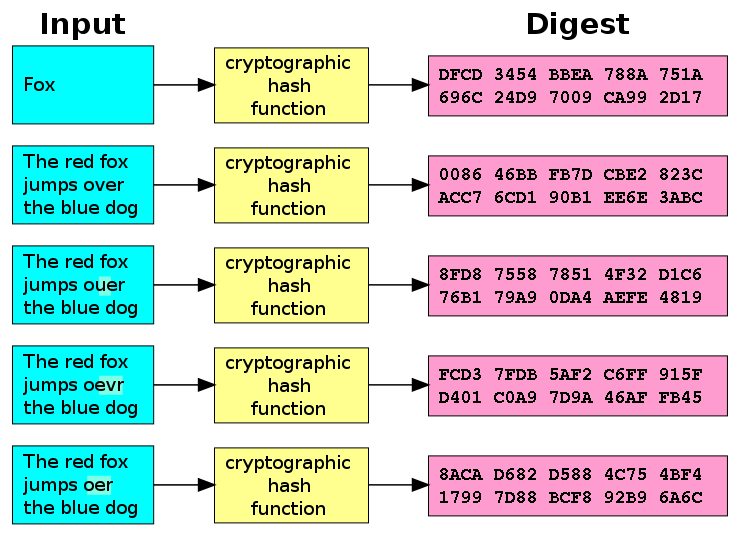
A hash function is basically a function, in mathematical terms, i.e. it translate a set of inputs into a set of outputs. For example, the mathematical modulo (division with rest classes) would be a hash function. In order to do cryptographic stuff, we need the hash functions to fulfill certain properties. We call those functions cryptographic hash functions, respectively:

• It is deterministic: The same message always will result in the same hash
• It is relatively quick to compute the hash value for a single message.
• It is infeasable to generate a message from its hash value except by trying all possible messages (brute force)
• It is chaotic: A small change to the input message should change the hash value so extensively, that the new hash value appears uncorrelated with the old hash value
• Collision resistant: It is infeasable to find two different messages with the same hash value.

For all we understand, hash functions are surjective, in a mathematical sense, but in reality we don’t know, just because of the properties given, it is infeasable to find a message that has a very specific hash. See figure \ref{ref:hash} for an example visualization of the SHA-1 function, a cryptographic hash function. Other viable crypto hashes include: The SHA family (Secure Hash Algorithm) - whereas SHA-3(“Keccak”) is the most recent one, and one should avoid using SHA-1, since some flaws have been found, that made it easier to find collisions in the algorithm.

\pagebreak

Symmetric Encryption

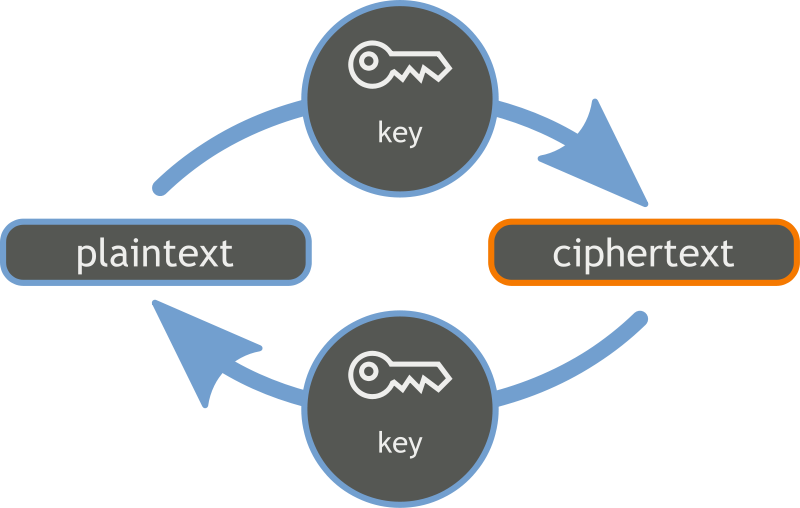
Symmetric encryption, is a type of data/text encryption, that makes use of a Symmetric-key algorithm <2>, very easy historic examples include: Caesar (Where the key is just the amount of letters you shift your message around the alphabet) or Vigenére <3>, but those are vulnerable to a few very basic attacks. Mainly those legacy encryptions are vulnerable to so-called known-plaintext attacks. If you can decrypt single messages, or parts of it, you can recover the key used to encrypt other messages. This is also the reason why Alan Turing was able to crack the Enigma machine <4>, used the WW2 Wehrmacht to encrypt their messages. (Common messages always included a small summary of the daily weather, as well as the common salute to the Nazi Führer Adolf Hitler). See figure \ref{ref:symkey} for a basic illustration.

Another important property, that goes for every primitive security related function (Hash functions as well as (a)symmetric key encryptions), is, that security through obscurity is not an option. That means, the “how to do stuff” should always be publicly available, and encryption functions should not rely on secrecy in the algorithm itself, but rather on mathematically difficult problems. (NP-Hard <5> ones to be exact)

The most common symmetric encryption algorithm currently is AES <6>, the advanced encryption standard. For the sake of simplicity, let’s just assume, it is secure and fulfills all the properties required.

\pagebreak

Asymmetric Encryption

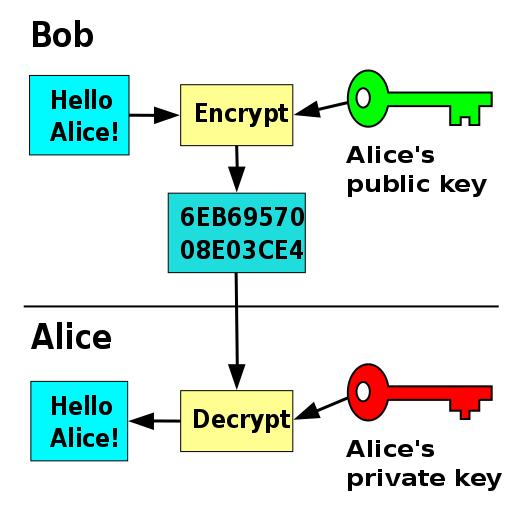
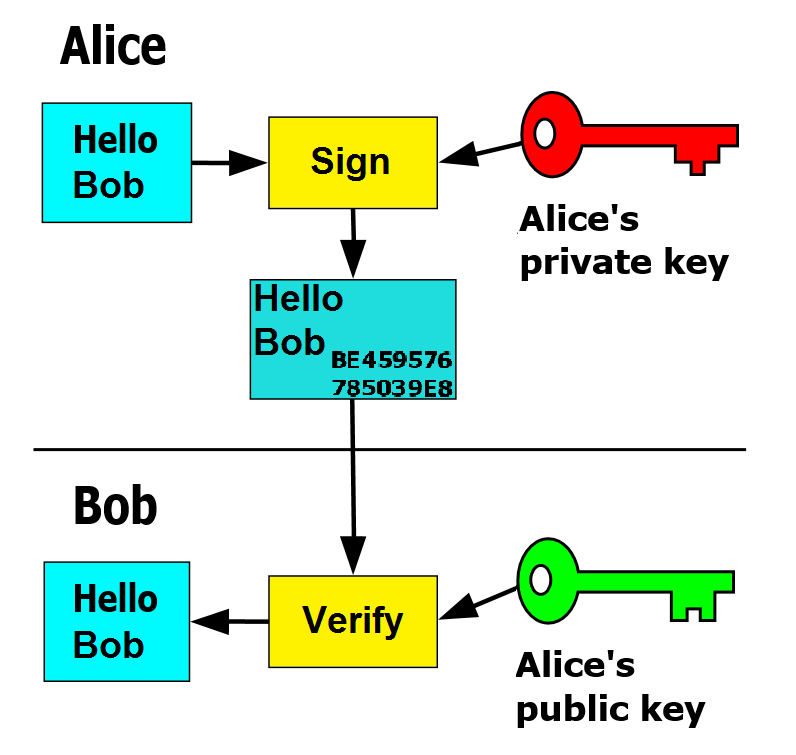
Whereas with symmetric key encryption uses a single key to do its deeds, asymmetric encryption relies on a key-pair <7>. The idea is, that everyone owns two keys, a public one, shared with the world, and a private one, kept in secret. The public one can be used for encryption, but not decryption. Messages can only be decrypted using the corresponding private key. So you can send messages using one’s, which the receiver can then decrypt with his/her own key. In addition, data can be signed with the private key, and later this signature can be verified with a public key. Without going too much into detail, how all of that works, you can see a visualisation on figure \ref{ref:pkey-encrypt} (Encryption) and figure \ref{ref:pkey-sign} (Signation)

Common algorithms used today are: RSA (based on large prime numbers) and ECC (based on elliptic curves) - Both rely on NP-Hard Problems, namely the factorization of prime numbers, and the ability to find discrete logarithms in the group of points of an elliptic curve (Which is not that hard for all curves, so not all curves can be used for ECC!)

\pagebreak

\pagebreak

Bitcoin basics

This section is to elaborate a few of the basic concepts we already discussed.

Transactions

As we are talking about bitcoin mainly as a currency (And are therefore ignoring the other implications of blockchain technology, good or bad, because they would more than just blow the boundaries) - Here is how basic transactions work:

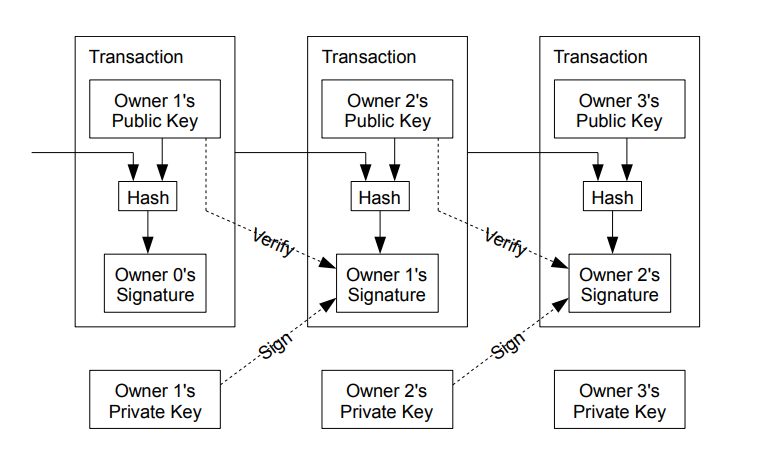
A digital currency is defined as a list of transactions, and in this case, a list of digital signatures. A transaction is made by signing a hash of the previous transaction, and the public key of the next owner. This “block” is added to the end of the currency (“Blockchain”) Now a payee can verify the signatures in order to verify the chain of ownership.

It is now very hard, without central authority, to verify that a spender actually owned the currency, before taking a transaction. We already established a chain of ownership, but we also need to save the time of transaction. For this, we use a technology called timestamp server. That is, a service that spits out hashed, unfakeable timestamps of the current date. (Kind of like holding a newspaper in a fotograph, in order to prove you shot it at a given day, but far more accurate) The basic point is: You have some kind of data, which you could not possibly have gotten your hands on, at a point in time, before stated. See figure \ref{ref:btc-chain} for a visualization.

Proof of Work

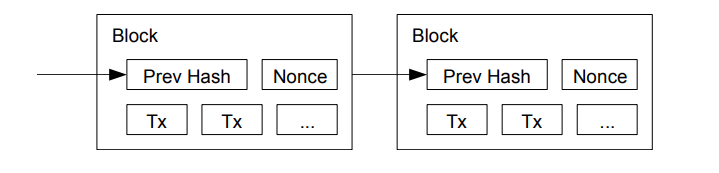
In order to implement a distributed timestamp service (Remember: We don’t want central authority, at all!) a proof-of-work is used. Each block contains a number, called Nonce (Short for number only used once!) which can be increased, until the hash of the block starts, or ends with a required set of fixed zero bits (Or any fixed number, though the implementation requires zeroes)

This also solves the problem of voting for which block to attach to the chain, because the majority is just determined by the group of nodes with the longest chain (i.e. they put the most effort in) - As long as the majority of the processing power is controlled by honest nodes, this will be fine, since frauding the chain will require to redo all of the proof-of-work challenges before, in order to restore the chain of trust, which is just not possible (alone that is!) See figure \ref{ref:btc-hash} for a visualization.

\pagebreak

Incentive

“By convention, the first transaction in a block is a special transaction that starts a new coin owned by the creator of the block. This adds an incentive for nodes to support the network, and provides a way to initially distribute coins into circulation, since there is no central authority to issue them.”

This is often compared with how gold mining works, and it is true, because the bitcoin network regulates itself in the difficulty of solving the proof-of-work challenges:

“To compensate for increasing hardware speed and varying interest in running nodes over time, the proof-of-work difficulty is determined by a moving average targeting an average number of blocks per hour. If they’re generated too fast, the difficulty increases.”